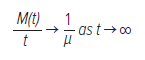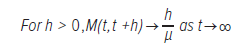Nearly a century ago, physicist Werner Heisenberg set the world of physics on fire with his declaration of the principle of Unbestimmtheit, or indeterminacy, at the centre of quantum mechanics.1 The core of Heisenberg’s Copenhagen doctrine was the idea that the statistical character of the new quantum theory established the final failure of causal determinism, because the new uncertainty principle established that although the precise momentum and velocity of subatomic particles could never be predicted from current behaviour, highly accurate probability distributions for potential particle behaviours could be precisely defined.2 Heisenberg’s argument against the notion of determinism in physics aroused a fierce response from, among others, Albert Einstein and Erwin Schrodinger that set in train a fierce debate about the relative role of causality and chance in modern physics.2
Analogous to this, the past five decades have seen an unceasing debate about the nature of the forces maintaining cardiac fibrillation.3–6 At the heart of this debate is the contest between those postulating fibrillation is maintained in a deterministic way, via the action of functional re-entrant drivers known as rotors, against the notion that fibrillation is sustained by more random forces, specifically multiple electrical wavelets stochastically wandering around the heart.7–10 Although other adjunctive mechanisms have been postulated to maintain fibrillation, including focal discharges and endocardial to epicardial dissociation, the core mechanistic controversy of the field, as in the realm of quantum physics, has been between notions of randomness and determinism.11–15
Traditionally, the rotor and multiple wavelet theories cast as two opposing theories of the mechanism of AF.3,16 In this paper, we review emerging evidence that, in AF, the rotor and multiple wavelet theories may, in fact, may intrinsically linked, with rotor formation and destruction able to be accurately modelled as a renewal processes.17 Renewal theory is a branch of probability theory that seeks to establish probability distributions for statistically independent events. Recently, we have reasoned that due to the disaggregated, turbulent nature of AF, the formation and destruction of re-entrant circuits could be modelled using renewal theory.17 Analogous to the way quantum mechanics seeks to predict accurate probability distributions for particle behaviour, we have used renewal theory to develop accurate probability distributions for the formation and destruction of re-entrant circuits in AF.17 We have shown that the renewal theory approach is robust in a variety of experimental conditions, and that the statistical signature of the renewal approach has been evident in all published data on phase singularity (PS) data published in the AF field.17
The renewal approach is quite different to existing approaches to deterministic modelling of AF because, at its heart, renewal theory does not seek to model particular rotor behaviours but, analogous to the quantum mechanical approach, seeks to understand the probability distributions. The power of this approach is that because of the disaggregated, uncorrelated nature of AF, the parameters of these distributions may be easier to accurately measure and model than developing precise models for each individual rotor and wavelet behaviours. Thus far, we have demonstrated it is possible to use the renewal approach in simulated, experimental and human AF.17,18
In this review, we provide a brief overview of contemporary understanding of the AF mechanism, to place the renewal approach into context; provide a brief background on the key scientific ideas and applications of renewal theory; explain the derivation of the renewal rate constants, from starting premises in the context of AF; review current experimental data supporting the renewal approach, highlighting the consistency of evidence supporting the renewal paradigm that has accrued from multiple laboratories in the past 20 years; place the renewal theory approach into context by highlighting other scientific domains where similar ideas have been successful; and identify potential opportunities to use this conceptual paradigm in basic and clinical research into AF mechanisms.
Contemporary Understanding of the AF Mechanism
Although the origins of the rotor theory of fibrillation began with the detection of circular electrical waves in AF by Sir Thomas Lewis more than 100 years ago, it was the demonstration of spiral waves by Winfree in chemical media, and subsequently in cardiac fibrillation, that placed rotors at the centre of modern fibrillatory dynamics.19–24 Contemporary understanding of the mechanistic role of rotors in fibrillatory dynamics has been pioneered by the Jalife laboratory. In a series of studies, the Jalife group defined a critical role for rotors as the drivers of both VF and AF.7,8,25–28 Rotors, by leading to the synchronised rotational activation of regions within their domain, have been proposed as the deterministic drivers of AF.3 Rotors are organised regions of high activation frequency, with the aperiodic turbulence of AF believed to occur via the breakdown of these high-frequency domains due to wave break in surrounding areas with slower conduction.29,30
However, support for the notions of rotors as drivers of fibrillation has not been universal. The pioneering computational studies of Moe and Abildskov postulated multiple wavelet theory as an alternative hypothesis to explain fibrillation.9,10,31 The key element of this theory was the premise that wave fragmentation and re-entry formation occurred via stochastic processes reliant on the inhomogeneous spatial distribution of tissue refractoriness. Support for the multiple wavelet theory in the experimental sense was led by Maurits Allesie, who failed to find evidence of rotors in human studies of AF.32 However, an important limitation of the multiple wavelet theory is that it was a descriptive rather than a statistical theory, and was thus unable to make testable quantitative predictions on the nature of fibrillatory behaviour, or provide links to the understanding of stochastic processes in comparable natural systems.33
Important adjunctive theories of AF have been the theory of focal discharges and endoepicardial breakthrough theories.11,13–15 These theories of AF have arisen due to the detection of spontaneous activations visible on the endo- and epicardial surfaces of the atrium in AF, postulating AF is sustained by repetitive focal activation or breakthrough of electrical activations between the myocardial surfaces.
The mechanistic debate about fibrillatory mechanisms has had a profound effect on clinical practice in the past decade, particularly for the treatment of AF. After the watershed demonstration that paroxysmal AF episodes could be triggered by pulmonary vein ectopy, the field has been revolutionised through the introduction of catheter ablation of AF. This approach has led to remarkable improvements in the efficacy of AF treatment.34–36
Despite this, pulmonary vein isolation (PVI) alone has only partially improved clinical outcomes in AF, with 50–60% of patients undergoing the procedure having at least some level of AF recurrence.37,38 In this context, there has been a push for new approaches to AF treatment that will improve clinical outcomes. Various strategies have been attempted, including ablation of complex electrograms, linear ablation and ablations of regions of high dominant frequency.39 All these strategies derived from observational evidence and were empirical rather than mechanistic, with none being consistently successful or reproducible at the present time.
In this context, the emergence of driver-based ablation has been an important development for the field.40 In 2012, Narayan et al. suggested not only the feasibility of using basket catheter mapping to identify rotors and focal activations driving AF, but also that these could be directly targeted via catheter ablation with improved patient clinical outcomes.41 However, other investigators have found that clinically mapped rotors are often temporally unstable and have not been able to achieve the same clinical benefit in the early focal impulse and rotor modulation (FIRM )studies, suggesting that current understanding of AF dynamics is incomplete and that new approaches to understanding fibrillatory dynamics are needed.42–44
At the present time, the field of fibrillatory dynamics is, in some sense, in a state of flux. Mirroring the debate on randomness and determinism in quantum mechanics, many leading figures in the AF field advocate for a continuing search for critical drivers sustaining fibrillation as the key to improving treatment. However, alternative voices argue that fibrillation is maintained by the activity of more random wavelet dynamics and that modifying the atrial substrate is more important. Regardless, it is clear that, at the present time, fresh ideas are needed beyond PVI in the catheter ablation field, which can only be achieved by better understanding of the fibrillatory mechanism.40
Recently, we demonstrated a potential common link that could potentially reconcile these two competing notions of AF, with the reproducible finding that unstable re-entrant circuits are born and destroyed at quasi-stationary rates.17 This can be defined and predicted using a branch of mathematics known as renewal theory. In the next section we explain and place into context this new finding and discuss the clinical and mechanistic implications for the development of new approaches to AF ablation.
Renewal Theory: An Approach to Understanding the Probability Distributions of Statistically Independent Events
Renewal theory is a branch of probability theory that seeks to understand and model the probability distributions of statistically independent events. The mathematics of renewal theory are somewhat complex, but the key principles and power of renewal theory can be understood with the help of some relatively simple analogies.
A classic example of a renewal process is flipping a fair coin, whose outcome is a head or a tail. If a coil is flipped once, the outcome (head or tail) is uncertain, but each may occur with a probability of 50%. If the coin is flipped 10 times, we would anticipate that although the most likely outcome is five heads and five tails, other outcomes are possible. However, if we flipped the coin 1,000 or 10,000 times, we would expect that the probabilities for heads and tails would be much closer to 50% each and can be estimated with great accuracy. Other examples could be rolling a dice or spinning a roulette wheel. On any individual realisation of the system, the outcome is very difficult to predict. However, if each of these systems is observed over many rolls or spins, the outcome probabilities will converge and the underlying probability distributions can be identified with a high degree of accuracy.
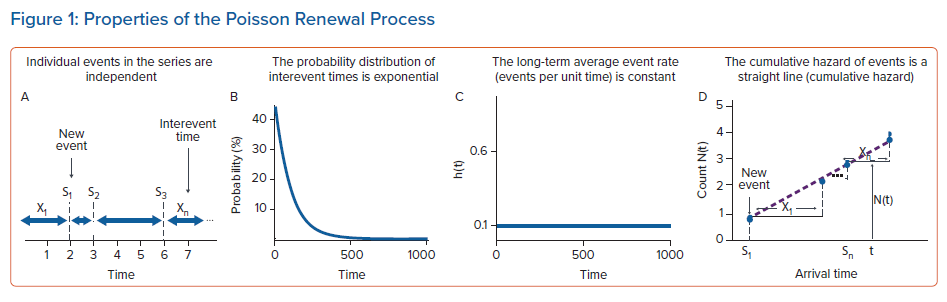
The same kind of notion, namely that statistically independent events will eventually converge to predictable probability distributions, is the basis of renewal theory. In a renewal process, although the timing of individual events is statistically independent, the long-term rate of the event occurrence arises from a specific probability distribution.45 The simplest type of renewal process is a Poisson process, in which the underlying event rate is constant (Figure 1). A characteristic of this type of renewal process is that interevent times follow an exponential distribution. Mathematically, it can be shown that if the interevent times follow an exponential distribution, then the underlying data generating process is a Poisson renewal process.46
The most familiar example of a renewal process illustrating convergence to an exponential distribution is radioactive decay. If we take a lump of a radioactive isotope, the timings of individual atomic decays are statistically independent, due to probabilistic quantum tunnelling events, but the decay rate converges to a stable rate over time. This produces characteristic decay curves for individual radioisotopes, enabling the decay rate to be determined with great accuracy, which is the underlying principle used in the construction of atomic clocks.
The key properties of a Poisson renewal process are summarised in Figure 1. Specifically: individual events in the series are independent (i.e. the occurrence of one has no bearing on the probability another event will occur); the probability distribution of interevent times is exponential; the long-term average event rate (events per unit time) is constant (constant hazard property); and the cumulative hazard of events is a straight line (cumulative hazard).
Mathematical Properties of the Poisson Renewal Processes
The renewal rate constants are readily calculated using a maximum likelihood-based approach by fitting to an exponential distribution using the following equation:
f(t) = λe−λt t ≥ 0 …(1)
where t is time and λ is the PS destruction or formation rate (referred to as λd and λf , respectively.17
In the case of interformation event times, the probability distribution yields the rate constant λf , which, in effect, is the long-term average formation rate of PS. In the case of PS lifetimes, this probability distribution yields λd, which is the average rate of destruction of PS. From the above equation, λf is derived from fitting a distribution to interevent formation times and λd from fitting a distribution to PS lifetimes. The close correlation of λf and λd calculated from event time distributions to that derived directly from PS time series data has been demonstrated.17
Renewal Processes in Nature
Renewal processes are a common motif in many other natural systems, ranging from radioactive decay to action potential firing in neurons and survival analysis.45,47,48 The Poisson process and exponential distribution are explained as inevitably arising in natural systems through the actions of multiple uncorrelated microscopic processes.45 The notion of statistically independent particle behaviour leading to predictable probability distributions, known as Stosszahlansatz, or the molecular chaos theory, underlies the kinetic theory of gases and is the basis of statistical mechanics.49
Rationale for a Renewal Theory Approach in AF
The defining property that sets apart AF from other arrhythmias is disaggregated, disorganised and turbulent electrical wave propagation in terms of wave propagation in space and time.50,51 This breakdown in coherence has been conceptualised as a conservative, non-dissipative form of chaos.52–54
In our study, we reasoned that, given the highly disorganised nature of AF, the formation and destruction of re-entrant circuits in AF could reasonably be considered statistically independent events.17 Our suggested rationale for this proposition is that because of the disorganised nature of AF, where wave propagation is disaggregated, events in one part of the chamber are effectively statistically independent of events in other parts of the atrial chamber. This has recently been examined by consideration of the autocorrelation of PS interval series, which converge to zero in the case of non-zero interval lags.55
If the formation and destruction of re-entrant circuits was statistically independent, we reasoned, by analogy with other systems where statistical independence is a key property, that the formation and destruction rates of re-entrant circuits in AF should converge to a constant rate.17 This would be expected to yield, under the principles of renewal theory, an exponential distribution of interformation times and re-entrant circuit lifetimes.
An interesting point to consider is why re-entrant circuits are intrinsically vulnerable to a process of generation and destruction. A clue may be found in the description of a rotor PS by Winfree. In his seminal monograph on spiral wave dynamics, Winfree provides a critical explanation as to why generation of new PS occurs: “[Because] every phase of the cycle [is] simultaneously always present… [the] timing of a stimulus is then no longer critical, whenever it will find somewhere a strip of tissue in the critical phase”.22
By the same explanation, because all phases of the cycle are simultaneously always present, any PS is intrinsically vulnerable to annihilation by an incoming wavefront. In an arrhythmia with disaggregated and spatially separated PS-like AF, the annihilation of the PS is thus statistically inevitable and accounts for the destruction of PS. This provides an explanation for the exponential-type distribution of PS lifetimes that is universally observed in fibrillation.
Evidence for a Renewal Theory Approach in AF
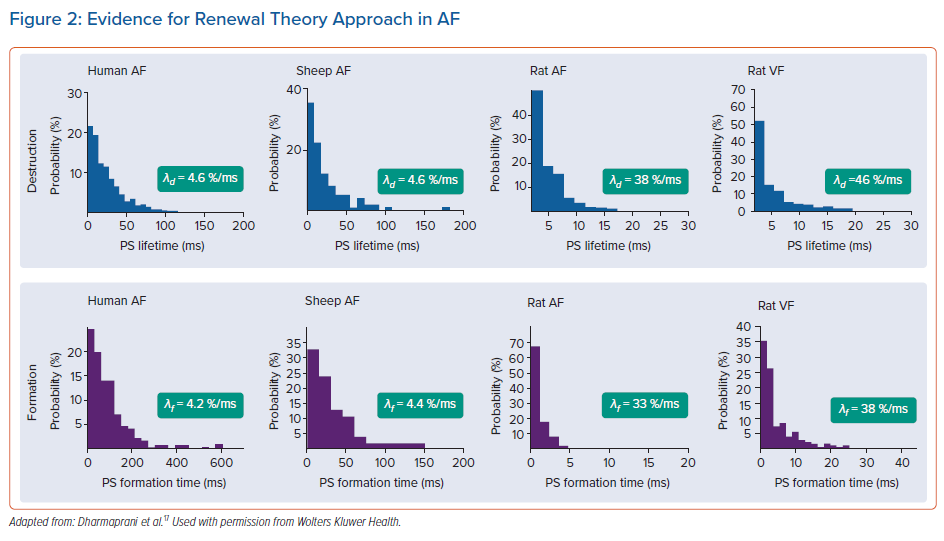
Recently, we studied interevent times for PS formation events and PS lifetimes in several systems, including included human persistent AF (basket catheter mapping) and rat AF (optical mapping) (Figure 2).17 The key finding of our study was that in all systems studied, the distribution of PS inter-formation event times and PS formation times were consistent with exponential distributions.
Consistency of Our Renewal Findings with Prior Published Literature
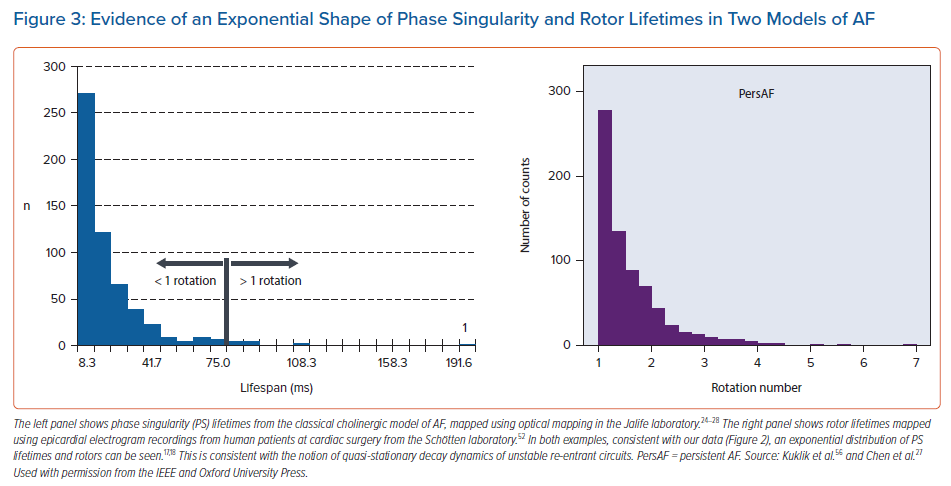
The powerful consistency of the renewal pattern identified in our experimental observations has received insufficient emphasis in the published literature on PS dynamics. In our study, we performed a systematic review identifying key studies in the field that had shown very similar findings of an exponential distribution of PS lifetimes, but where this pattern had not been recognised by the investigators at the time (Figure 3).
The first study was from the group of Chen et al., using the classic cholinergic model of AF in the explanted sheep heart, mapped with optical mapping.27 Chen et al. demonstrated that PS in this model had a mean lifespan of 19.5 ± 3.8 ms, and examination of the published histogram of the data from that paper showed the characteristic shape of an exponential distribution.27 Similar findings were observed in another study.56 In that study, rotor lifetimes were examined in epicardial mapped recordings from patients undergoing cardiac surgery, in both persistent and paroxysmal AF.56 Very similar findings have been observed in basket catheter recordings by Child et al.57 We have also identified the same pattern of PS lifetimes in VF from multiple distinguished laboratories.29,58–61 The convergence of renewal rates of PS formation and destruction conforms with models of spiral wave chaos showing quasi-stationary steady state numbers of PS.62
A key question is why this exponential pattern of PS lifetimes repeatedly and reproducibly arises in both AF and VF. We reason that this is due to the disaggregated and turbulent nature of wave propagation that defines AF. In essence, because PS formation and destruction events are determined by local electrical activity in particular regions of the atrium, they become statistically independent of PS formation and destruction events at spatially separated regions of the atrium. Over time, this statistical independence yields a quasi-stationary rate of decay of formation and destruction times, which accounts for the reproducibility of the renewal paradigm.
Rationale for Focusing on Phase Singularities
The rationale for focusing on PS in AF is that these are located both at the heart of re-entrant circuits and at the free ends of wavelets during fibrillation. Gray et al. identified some key rules regarding PS based on principles of topology: phase lines cannot intersect; PS are joined by other isophasic lines to PS of opposite chirality or non-conducting boundaries; and PS form and terminate as oppositely rotating pairs.8
In our study, we reasoned that because PS are effectively subject to a quasi-stationary rate of decay, an exponential distribution should be observed in both PS overall and the subset of PS that are longer-lasting and have undergone one or multiple rotations.17 In fact, this is what we observed.17 We also noted that groups who have focused on PS arising only from re-entrant circuits that have undergone a complete rotation also find an exponential distribution of PS lifetimes. In effect, this would suggest that PS at the free ends of wavelets and those at the centre of rotors are effectively one class on a biological continuum, rather than being separate classes of re-entrant circuits.
Renewal Theory: A Conceptual Approach to Unify AF Mechanisms?
On the one hand, the characterisation of AF as a renewal process is intuitive and natural, given the essentially disaggregated nature of wave propagation in AF in space and time. An important concept is that renewal of PS provides a crucial link between the multiple wavelet and rotor theories of AF. An intriguing possibility that could be considered is that the renewal approach could link existing concepts of a multiplicity of AF mechanisms and suggests the possibility of a single unified AF mechanism.6
In Moe’s original conceptualisation of the multiple wavelet theory, although re-entry was recognised to occur in qualitative terms, it had no quantitative formulation.10,31 Moe’s simple computational model could not develop spiral waves, which are a defining property of re-entry in cardiac fibrillation.63 On the other hand, the rotor theory emphasises the role of re-entry as the driver of AF, with the chaotic turbulence of the arrhythmia explained as arising due to wave break at regions of slow conduction. Again, the classical rotor theory does not provide a quantitative architecture to measure the process by which this occurs.64
The key missing piece of the rotor theory of AF has been that it has not provided a mathematical framework to model how rotors are formed and destroyed to sustain the arrhythmia over time. Characterisation of PS formation and destruction as renewal processes provides a quantitative framework to model these processes. From a mechanistic point of view, this may be appealing on several levels because it provides a robust theoretical foundation in renewal theory. Renewal theory is a branch of probability theory to model events that occur randomly in time, with the basic assumption that the times between successive events are independent and identically distributed.65 Renewal theory provides a deep mathematical structure to enable predictions about future behaviour.
At present, in our current conceptualisation of renewal theory, we have not directly addressed the focal discharge or endoepicardial theories of AF because we have not had access to datasets in AF that were used to identify these potential mechanisms. However, we would hypothesise that renewal rate constants on the endoepicardial surfaces could potentially be correlated in individual atria; in relation to the focal discharge theory, under the renewal conceptualisation of AF, we would postulate that such focal discharges should converge to occur at temporally stable rates due to the fact they would not be expected to be correlated in space or time.
The consistent evidence supporting renewal theory would potentially suggest that the fundamental mechanism of AF is not one of AF as sustained by driving rotors, but that AF is, in fact, sustained by a repetitive cycle of PS annihilation and regeneration.17 In this respect, renewal theory fills in a key gap in the rotor theory of AF. There are two important ideas from renewal theory useful to from characterising PS formation and destruction. The first of these ideas is that the elementary renewal theorem, that limiting the mean average rate of events, is 1/μ:65
where t is time, M(t) is the number of events at time t, and μ is the inverse of the average rate. In the context of rotor formation and destruction, this means that the mean rotor formation (or destruction) rate should converge to a constant rate.
The second ideas is the renewal theorem (i.e. that the expected number of events in a time interval is asymptotically proportional to the length of the interval; Blackwell’s theorem):65
In the context of rotor destruction, this would mean that the number of rotors formed (or destroyed) in a time interval h is proportional to the length of h, where h represents the interval of time.
Potential Applications of the Renewal Paradigm in Mechanistic Studies
The renewal process paradigm could be used in several contexts to quantify the dynamics of fibrillation. The renewal rate constants could provide a powerful means to quantify the relative effects of ion channel modulation via drugs, electrical and structural remodelling and the anatomical effects of variations in microarchitecture, as well as to quantify the effect of ablation on fibrillatory dynamics. Because the renewal rate constants are a consistent feature of the biology of fibrillation, identifying their determinants becomes important to understanding the AF mechanism. It is likely that varying extents of fibrosis and gap junction coupling, which contribute to differently perceived patterns of fibrillation, could manifest these changes by alterations in the renewal rate constants under these types of alterations in underlying determinants of AF physiology.66 Renewal theory may provide a useful way of quantifying the position on the spectrum of potential physiological fibrillatory dynamic patterns, as recently envisaged by Handa et al.66
A specific key area of future research is determining the relationship between AF renewal processes and AF persistence and termination. In the clinical context, the progression of AF from short-lasting episodes to a longer-lasting persistent pattern of AF is associated with poorer long-term outcomes, including higher rates of stroke and mortality.67 In computational models of AF, changes in substrate characteristics are associated with changes in the number of PS and PS lifetime.68 However, these processes have been described in mainly qualitative terms.69,70 It would be reasonable to hypothesise that changes in the rate constants of PS formation and destruction may be useful in predicting the persistence or termination of AF.18
A potential strength of renewal theory is that it may well be able to provide a way to accurately quantify differences in AF pathophysiology where AF is seen to arise from different mechanistic camps (e.g. hierarchical or non-hierarchical mechanisms). In our analyses thus far, we have found the renewal theory approach to apply universally in all systems and patients studied. It would be of great scientific interest to understand the differences in renewal rate constants in different forms of AF where the causes are perceived to be different.18 We are prospectively studying these issues in the RENEWAL AF study, which will prospectively recruit patients with different clinical classifications of AF, allowing for a comparison of renewal rate constants to clinical AF features.17,71
The renewal rate constants have several attractive properties. Because they have a defined distributional type, they can be accurately measured via repeated sampling. Under the central limit theorem, the maximum likelihood estimate for the renewal rate constant will rapidly be able to be estimated with repeated sampling of PS. Due to the short-lasting nature of PS, it is anticipated that it will take a relatively short period of time to gain a relatively accurate and precise estimate of the renewal rate constant. The renewal rate constants will be expected to have properties of temporal stability. Due to the quasi-ergodic nature in which the uncorrelated PS formation and destruction events occur, over time it is anticipated that renewal rate estimates will converge to quasi-stationary rates. This is analogous to the way the heads–tail, dice and roulette examples converge to accurate estimates once the system is sampled for sustained periods of time.
Future Applications of Renewal Processes in Clinical Settings
The establishment of λf and λdas a universal rate constant of PS formation and destruction has several potential applications for clinical practice. First, these constants provide readily measurable clinical markers of global AF dynamics in ongoing fibrillation, directly related to the underlying AF mechanism. In this regard, they may potentially emerge as clinically reliable markers of AF persistence and progression. A more detailed understanding of the spatial distribution of the renewal rate constants in the atrium and their relationship to atrial microarchitecture could potentially inform novel approaches to AF ablation. The fact they arise consistently and reliably and are theoretically temporally stable could make them more reliable markers of AF dynamics than other measures, such as dominant frequency,72,73 entropy74,75 or quantitative electrogram complexity analyses, which can suffer from temporal instability.38,76 A key to utilisation would be the capacity to directly estimate these parameters from surface ECG data, which is the subject of ongoing research.71 To enable the development of these as reliable physiological markers, it would be ideal to be able to develop approaches to predict λf and λdfrom surface ECG data to enable longitudinal non-invasive measurement of rotor formation and destruction rates in individual patients.
In addition, the efficacy of other ablation methods beyond that of PVI particularly for patients with persistent AF have not been proven.77 Although additional lesion sets beyond PVI have been increasingly adopted for these patients, success rates for these adjunctive approaches for these patients remains uncertain.78 Moreover, if extra lesion sets beyond PVI are created, there are no current measures that could be undertaken during the procedure to monitor the clinical efficacy of the chosen method. The renewal paradigm may provide a useful explanation as to why potential approaches to map ‘drivers’ of AF have so far been inconsistent. The use of renewal rate constants as a marker of acute success during catheter ablation procedures could potentially overcome this limitation. Real-time modulation of intraprocedural λf and λdcould be used to measure effectiveness of PVI, with or without a chosen non-pulmonary vein trigger approach for patients undergoing catheter ablation for AF. Studies are underway to define the spatial variation of the renewal rate constants in the atrium.71
Conclusion
To date, AF mechanisms remain unresolved. The characteristic turbulent and random nature of AF has so far led to a lack of quantitative measure to analyse AF dynamics. Renewal theory provides a new mechanistic description of AF being sustained by a repetitive cycle of PS annihilation and regeneration, which, uniquely, also allows quantitative assessment of AF dynamics that is reproducible and consistent across different measuring modalities.
Clinical Perspective
- The mechanisms underlying AF maintenance remain unclear.
- Renewal theory is a new quantitative framework to analyse fibrillatory dynamics in AF and has the potential to reconcile these theories by providing governing equations for the formation and destruction of phase singularity.
- Renewal theory could potentially be used to monitor AF progression in patients, guiding decisions for timing of AF ablation; and to allow individualisation of ablation strategies in patients with different AF phenotypes.
- Spatial characterisation of the renewal rate constants throughout the atrial chamber might allow the development of strategies that could more reproducibly lead to the termination of AF and long-term maintenance of sinus rhythm.