Primer on Machine Learning in Electrophysiology

Artificial intelligence (AI) has recently gained popularity, becoming a buzz word in the fields of science, technology, engineering and mathematics. AI aims to teach a computer how to replicate human intelligence to perform human tasks. Machine learning (ML) is a subset of AI that uses data to teach a machine how to imitate human behaviour. The overall goal of ML is to have a computer perform a task that a human performs, based on prior collected data, with high accuracy, quickly and automatically. The ‘holy grail’ for ML is to have a computer outperform the prediction ability of humans. While the purpose of ML is clear, ML has no standard model and is almost exclusively task-specific.

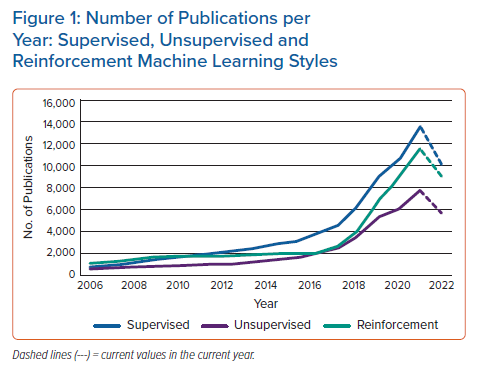
ML performs statistical operations on data sets to learn underlying patterns. The three most common ways a machine can learn are through supervised, unsupervised and reinforcement learning. Each way of learning is specific to the available data and/or the operators’ goals. Supervised learning uses labelled data to understand the correlation between inputs and outputs. Unsupervised learning finds hidden patterns within data sets. Reinforcement learning determines optimal decisions based on feedback from the interaction between an agent and an environment. In 2021, there were a total of 13,646, 7,774 and 11,567 publications specifically under the labels ‘supervised’, ‘unsupervised’ and ‘reinforcement’ learning, respectively, according to the Scopus database (https://www.scopus.com). The number of publications of these three learning styles have been steadily increasing, picking up momentum from approximately 2010 (Figure 1). In this primer review article, we focus on supervised and unsupervised ML, as reinforcement learning is an algorithm that has not yet found applications in healthcare, particularly in cardiac electrophysiology (EP).

The earliest ML models are linear and non-linear least squares regression, which aim to learn functions of a defined form from data, and have been around for centuries.1–3 In terms of modern ML, the first application is considered to be the mathematical model depicting the activity of interconnected neurons described by McCulloch and Pitts in 1943.4 This model has progressed and is known today as an artificial neural network (ANN or NN). In 1959, Samuel created a NN type model, which used a form of reinforcement learning to teach a computer to play checkers.5 This work showed the feasibility of a computer mimicking human learning. Since then, many other ML models have been developed that have attempted to model human intelligence.

In the field of healthcare, ML has been leveraged to better equip clinicians and patients with the ability to make confident decisions for better care. ML is in the infant stages of being implemented as part of clinical practice and typically entails the use of data derived from sources such as electronic health records (EHR), ECGs and implantable devices. The amount of medical data available is rapidly increasing as new technologies are being incorporated in clinical and everyday settings, such as smartwatches capturing biological signals. For instance, the onset of Parkinson’s disease could be predicted in individuals 75% of the time before an actual diagnosis is made using an ML model that operated on wireless signals collected from remote sensors.6 While these advances are promising, much work needs to be done to establish and expand the use of ML in healthcare.

In the field of cardiac EP, ML is an active area of research, in the early testing phase for adoption into clinical practice for specific applications. The cardiac EP community has shown an increased interest in the subject. Clinical practitioners are eager to understand what ML entails and participate in determining the usefulness of these technologies in their practice and decision making. The overall goal of this ML primer review is to provide an overview of supervised and unsupervised ML models and to explain how they operate and how they have recently been used in cardiac EP studies.

Machine Learning Models

Supervised Learning

Within ML, the most common type of learning is supervised. Supervised learning uses data that has both inputs and outputs. Other names for input data are ‘features’ or ‘independent variables’ and likewise, output data are called ‘labels’, ‘targets’, ‘dependent variables’, or ‘ground truth’. Simply put, supervised learning uses data sets with both x and y variables, and the goal of a supervised learning algorithm is to optimise a model to predict y from x. Due to the nature of big data, supervised ML models usually operate on a large number of input features to determine a singular or few output values. Typically, supervised learning models contain parameters, commonly called learnable, that are adjusted via an optimisation procedure during the learning process. For supervised ML models, there are two types of tasks which they can learn to perform. The first task is classification, where output data and, accordingly, the ML models’ predictions are discrete, representing different classes (i.e. 0/1; true/false; A/B/C, e.g. from 12-lead ECG, predict AF, occurrence – yes, or no?). The second is regression, where output data and the corresponding ML models’ predictions can be any continuous numerical value (i.e. 0.84; 11.3%; -2.6 kg, e.g. from an echocardiogram, what is the volume of the left ventricle?). Below we focus on the most common supervised ML models, how they operate and how they have recently been applied in cardiac EP studies.

Typical Supervised Learning Models

Least Squares Regression

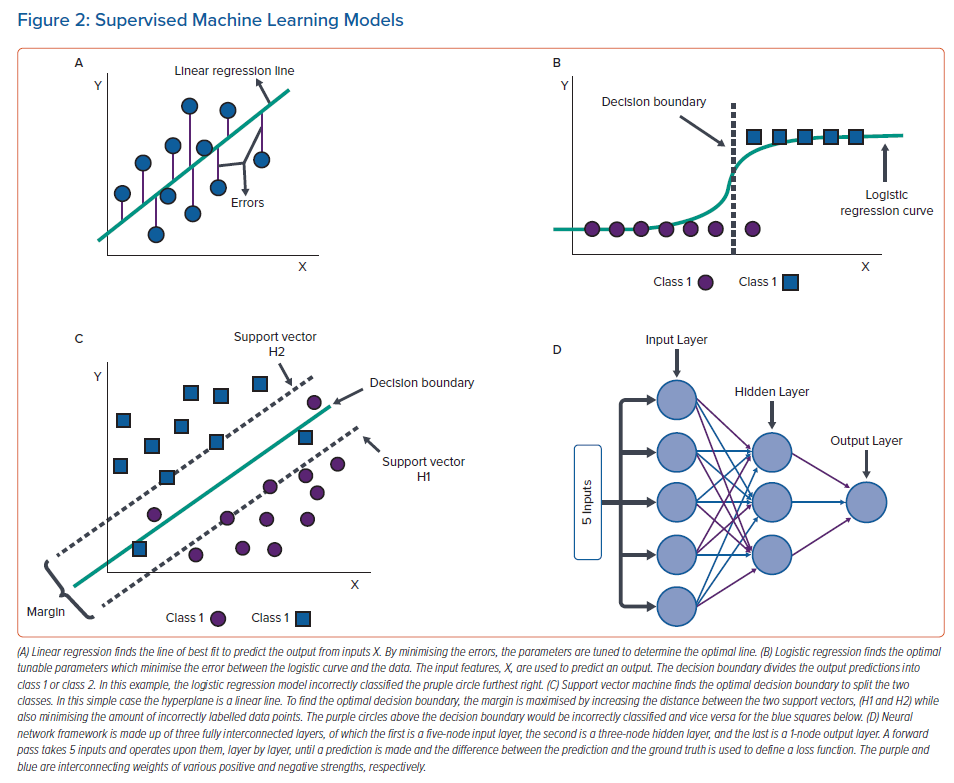
Least squares regression operates by minimising the square of errors between ground truth and the model’s predictions. These models are of a defined form with learnable parameters that are subject to an optimising procedure (i.e. a linear function is of the form y = mx + b where m and b are learnable parameters). The simplest case of least squares regression, linear or multilinear regression, is an ML method that fits a linear equation to input data to predict an output. It assumes that all the features in a data set are linearly proportional to the outputs and minimises the errors in determining the linear relationship. Ridge regression and lasso regression are two common variations of linear regression which aim to minimise the error of a linear regression model by also minimising or completely removing the effects of low correlating features on the predictions; this is done by introducing penalty terms to the linear regression model. Logistic regression is a non-linear least squares regression which fits a logistic function to data by minimising the error between the correct and predicted output labels. Typically, logistic regression is used for binary classification where the ground truth is either class 1 or class 2 and the model incorporates a decision boundary (usually 0.5) to classify the predictions to either class. Linear and logistic regressions tend to work wonderfully on many data sets and often outperform more complex ML algorithms, but as powerful as they tend to be, they are often too simple to capture the behaviour of complex systems due to the rigidity of defining the model’s structure.7,8 Illustrations of linear and logistic regressions are shown in Figure 2A and B, respectively.

In cardiac EP, there have been several studies using least squares regression to predict different outcomes, ranging from predicting the likelihood of AF recurrence to what wattage catheter ablations perform better.9–15 Least squares regressions have been preferred in these studies because they are easy to implement, can learn the key features (from EHR data/clinical covariates or ECG biomarkers, or in performing survival analysis), and are interpretable. Least squares regressions are often included with other ML algorithms to help find the best performing model. For example, in the study by Jia et al. lasso regression was first used to determine the most relevant features, which were next used in a logistic regression to predict AF recurrence within a year post radiofrequency ablation.13 These two least squares regression methods performed well in conjunction because the penalty terms in lasso regression helped eliminate low corresponding features and logistic regression learned on the most important features, ignoring noise induced by low corresponding features. Another example is by Howell et al. who applied a lasso regression model on short-term cardiac resynchronisation therapy (CRT) responses to identify CRT patients who most needed early heart failure care.15 Least squares regressions have also been used in simulation cardiac EP studies: Maleckar et al. showed that logistic regression predicted the risk of arrhythmia in post myocardial infarction patients from late gadolinium enhancement MRI (LGE-MRI) and patient EHR; the simple logistic regression model slightly outperformed other more complex ML models.12

Support Vector Machines

Support vector machines (SVM) are ML models that typically solve classification problems by defining a decision boundary to split data into different classes.16 The decision boundary is defined as a plane or curved surface in the space of the input data to differentiate the classes. In the simplest binary case, the decision boundary is a linear discriminator and is called a hyperplane. Two support vectors (H1 and H2) are determined as an up and a down shift from the decision boundary and are defined by data points. The distance between the two support vectors is called the margin, which is a variable used in the optimisation procedure. Using an iterative process, the optimisation procedure maximises the margin and minimises the amount of incorrectly predicted labels. Variations of SVM exist to classify complex non-linear data, where the hyperplane is typically replaced with a (bending) hypermanifold. An illustration of SVM is shown in Figure 2C.

SVM have been used in cardiac EP studies to accomplish various tasks from predicting the presence of AF in ECG to forecasting which patients would have a positive outcome from cardiac resynchronisation therapy.17–21 SVM were preferred in these studies because they are easily interpretable, are able to handle high-dimensional data and can be used in conjunction with other ML models. Overall, SVMs are one of the easiest ML models to implement. An example of SVM in cardiac EP is the study by Nguyen et al. in which ECG features were extracted with another ML model, and then subsequently used as inputs to an SVM for prediction of AF from a single-lead ECG.19 Shenglei et al. applied SVM to predict, from LGE-MRI and ECG features as well as clinical data likelihood of sudden cardiac death or heart transplant in patients with dilated cardiomyopathy and low ejection fraction.18 Additionally, Narayan et al. used an SVM, which outperformed a neural network, to predict future ventricular tachycardia and mortality within 3 years from ventricular monophasic action potentials.20 Comparatively, SVM performed well because the data was of low dimensionality.

Artificial Neural Networks

While NNs can be used in specific cases in unsupervised learning, typically, they are used to solve supervised learning problems for both regression and classification predictions.22,23 For the simplest supervised learning version of NN, the multilayer perceptron model, a type of dense NN, uses numerous layers of nodes interconnected through different strengths/weights to represent the synaptic connection between neurons. Typically, the input data are operated upon, transformed, and then passed to the next layer as its input. This process is repeated through all layers until arriving at the output layer, which is the prediction. Most commonly, a loss function is defined as the difference between prediction and ground truth, and through a process called gradient descent/backpropagation, the strengths/weights connecting layer to layer are updated iteratively until the optimal model is achieved when the loss function ceases to decrease. In addition to the multilayer perceptron, there are other types of NN developed to learn on different types of data sets.

Originally derived from studying the biological process of light activating specialised cells in a cat’s eye, convolutional neural networks (CNN) overlap learnable filters (multi-dimensional array of weights) on regularly spaced data, like image pixels or ECG signals, to learn common features.24 Gradient descent/backpropagation is performed to optimise the model by adjusting the learnable filters. Likewise, recurrent NNs are a form of dense NN that handle series data, typically time series, to learn important features as they evolve. Some of the most popular recurrent NN styles are long-short term memory and gated recurrent unit, which incorporate a framework that retains only the most important information from prior points in the series.25,26 NNs have become the most popular type of ML models. As they typically require very large data sets to learn from and can take a long time to train, it is common to first apply other simpler ML models to see if they can solve the problem at hand. Figure 2D shows a simple illustration of an NN.

In a recent explosion in popularity, NNs are being widely used in cardiac EP, from predicting AF or congestive heart failure from heart rate variability biomarkers, to predicting the presence of acute myocardial infarction from an ECG.27–44 NN models have been preferred in these studies because they can practically operate on any data type, and they inherently learn feature importance and the relationships between features. These studies have demonstrated the advantages of NN in handling raw ECG data, raw LGE-MRI signals, electroanatomic mapping (EAM) data, and overall, in learning from high dimensional complex data. An example of NN in cardiac EP is using a CNN on a 12-lead ECG to predict the new onset of AF within a year from baseline ECG in patients with no prior history of AF.43 Because the filters in a CNN can capture key patterns in the ECG, this approach was able to distinguish the signature of early remodelling of the atrial myocardium. Another study trained a CNN on registered ischaemic scar masks from LGE-MRI to segmented CT images to learn to detect the presence of ischaemic scar tissue from CT images alone.32 Popescu et al. developed an approach to risk assessment of sudden cardiac death due to arrhythmias which combined NNs with survival analysis to construct patient-specific survival curves offering accurate predictions of up to 10 years; the methodology allowed for estimation of uncertainty in predictions for the input data.40 The NNs learned on raw cardiac images and clinical covariates, and with this approach, significantly outperforming standard survival models.

Random Forest

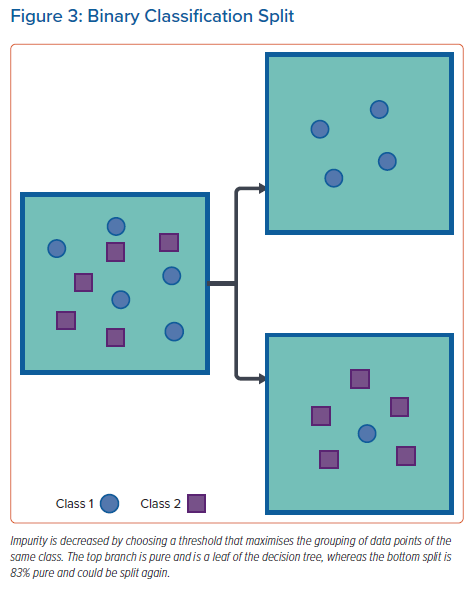
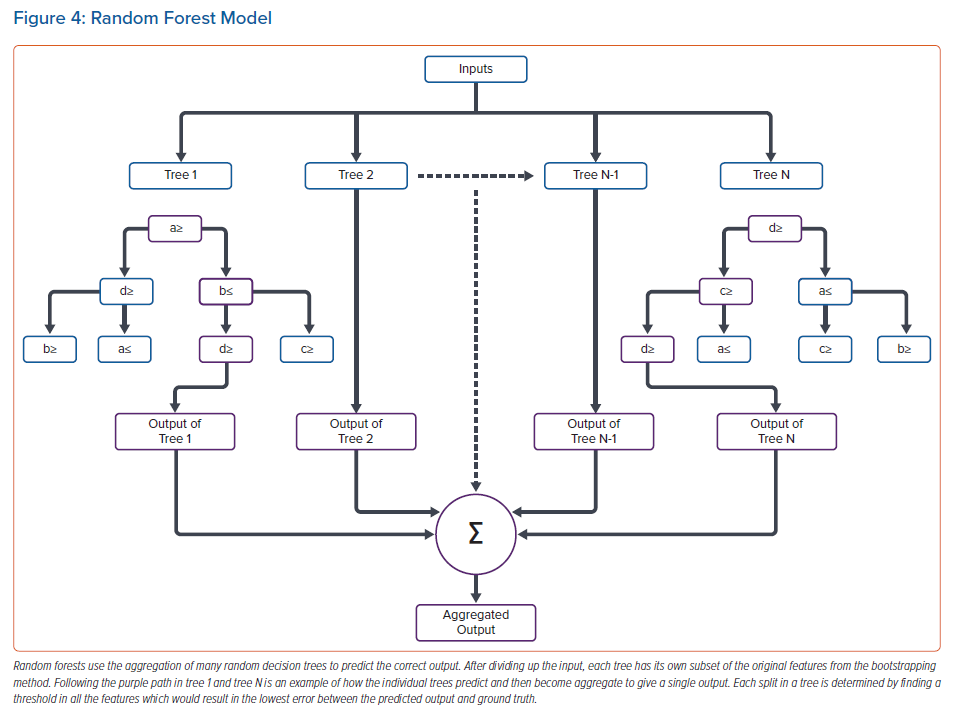
Random forest operates by defining many thresholds, or branches, in a multitude of randomly determined decision trees to predict either classification or regression outputs, typically based on majority rules or averaging.45 To create many distinct random decision trees, a method called bootstrapping is used, which randomly selects features in the data set to create a sub-data set for training a distinct decision tree, which is subsequently aggregated with other distinct decision trees.46 Aggregation of many distinct trees increases the model’s ability to correctly predict, but also makes the model more complex. For binary classification, each split in an individual decision tree decreases the impurity of the subgroup, i.e. maximises the number of similar classes in the next set of branches (Figure 3). Typically, each separation operates to minimise the Gini index or entropy in each split. Minimising either value incorporates measuring how much information is gained by setting a threshold and grouping the data. Similarly, for regression problems, each split in the tree finds the minimum difference between predictions and ground truth (minimal square of error) for each input individually to determine the optimal split. For both processes, splitting continues until the maximum number of branches/splits is reached or until splitting quits optimising the branch. The last splits on a branch are called leaves. An example of a random forest model is shown in Figure 4.

Random forest algorithms are a popular approach in cardiac EP and have been used in studies ranging from predicting left atrial appendage flow velocity to predicting 30-day mortality post ST-elevation myocardial infarction.47–55 Random forest models were useful in these studies because a decision path to the correct prediction could be found in the majority of distinct trees. Random forest models have been shown to be particularly useful in providing interpretability due to each split being a defined threshold that offers insight. These advantages were demonstrated in using post ST-elevated myocardial infarction EHR data to predict mortality; the algorithm was able to find proper splitting because there were many features with high importance that alone were able to correctly predict outputs.55 Rouhi et al. showed that through extracting custom features from ECGs, a random forest model was able to detect AF.48 Pičulin et al. were able to predict the progression of hypertrophic cardiomyopathy 10 years out using a random forest model.52 Additionally, both of these studies by Rouhi et al. and Pičulin et al. offered model interpretable, i.e. a meaningful insight into the model’s decision making. Shade et al. used a random forest model that combined in silico data for substrate arrhythmia inducibility with imaging and clinical data to predict risk of sudden cardiac death due to arrhythmia in sarcoidosis patients.51 Random forest was able to predict well on this data set because it can split the multimodal data many ways to inform its decision and incorporate the correlation between the different data types.

Unsupervised Learning

Unsupervised learning aims to learn the underlying patterns within a data set without explicitly knowing how data is correlated, i.e. to find patterns within data x without having the labels y. Typically, unsupervised learning aims to cluster instances into distinct groups which are most similar to each other. Defined clusters are often used to infer labels for use in a supervised machine learning model. Another common form of unsupervised learning is dimensionality reduction, which aims to transform the data set to reduce noise and size. Typically, dimensionality reduction is used in conjunction with another model to improve performance. Altogether, unsupervised learning is ideal for learning unbiased information about data and can function on data without many data points (i.e. data sets with a low number of patients in the cohort). Here, we discuss some of the most popular unsupervised ML models.

Typical Unsupervised Learning Models

k-means

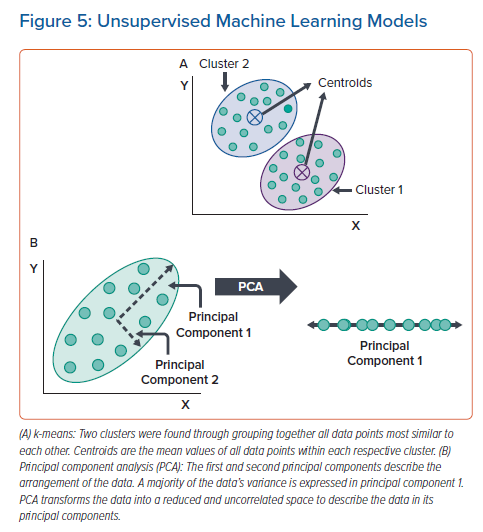
k-means is an unsupervised ML model that aims to cluster data entries that are most similar to each other.56 Prior to training the model, a set number of clusters, k, are chosen to fit the data set and are each given an initial centroid location in the data space. Each cluster is defined by conglomerating all data points whose Euclidean norm is closest to the clusters’ centroid. Through minimising the distance between all data points in a cluster and the cluster’s centroid, the centroid’s location is updated in an iterative manner until the data points stop swapping between clusters or a maximum number of iterations is reached. Typically, k-means is easy to implement and is a powerful tool for clustering separable data, but is defined by a strict algorithm and may not be able to capture information from complex data sets. Additionally, k-means is affected by outliers. An example of k-means is shown in Figure 5A.

In cardiac EP, k-means clustering has been used in studies, from finding clusters in data on heart rate variability, to finding scar tissue by clustering similar LGE-MRI pixels together.57–62 Unsupervised k-means models were preferred in these studies because they are easy to implement, are highly interpretable and perform unbiased learning. These studies have demonstrated the advantage of k-means in operating on small data sets and in discovering unknown underlying patterns. An example of k-means in cardiac EP was the study by Schrutka et al. which used measurements from electrocardiographic imaging (ECGI) and common 12-lead ECG to cluster patients with cardiac amyloidosis.60 k-means determined patterns of overlapping information between ECGI and ECG measurements that help to create a cardiac amyloidosis diagnostic test. In another study, k-means was performed on atrial ECG and EAM data to discover five distinct clusters in persistent AF patients that could be used for a more complete characterisation of the persistent AF substrate.62 Wang et al. applied k-means to MRI data to find if left bundle branch block precedes dilated cardiomyopathy.57 Two clusters were found with features that distinguished patients who did and did not have dilated cardiomyopathy preceding left bundle branch block. These findings could better equip clinicians with predictors to CRT success.

Principal Component Analysis

When data is not easily separable or there are too many features in the data for another ML model to fit, principal component analysis (PCA) can separate data, reduce noise, and reduce the number of features in the data.63,64 While PCA does not separate data into clusters, like k-means, it can be used to enhance the performance of another model. To separate the data set into principal components, a correlation matrix is defined that describes how much each feature of the data set correlates with another. Typically, PCA operates using either Eigen or single-value decomposition of the correlation matrix, which calculates the principal components describing the arrangement of the data. To reduce the data and remove noise, the original data set is transformed to an uncorrelated space by using the lowest principal components. Once data is reduced/transformed, it is common to either perform standard statistical measures or other unsupervised ML models to discover important patterns in the data set. An illustration of PCA is shown in Figure 5B.

PCA has been used in multiple cardiac EP studies ranging from predicting different atrial arrythmias to predicting congestive heart failure.34,59,61,65–67 PCA was preferred in these studies since it reduced the data size to help other ML models learn the most important features within a data set. Balaban et al. applied PCA to a segmentation of the left ventricle to determine the lowest principal components of the ventricles’ shape for use in a Cox-lasso regression model to identify patients at the highest risk of sudden cardiac death, aborted sudden cardiac death, or ventricular tachycardia.66 PCA was applied by Selek et al. to predict congestive heart failure from heart rate variability biomarkers and other measurements by using only the lowest principal components.65 PCA has been applied to simulated vectorcardiograms to find the most important features so that patient-specific activation maps can be reconstructed.67

Conclusion

In this primer, we presented the most popular and most used models in cardiac EP research – ‘supervised’ and ‘unsupervised’ ML. In addition to describing and explaining the models, we included a rationale for their use in cardiac EP studies. Our hope is that this primer will help the cardiac EP community to understand how ML is used to address problems in arrhythmias and cardiac EP, and to provide a glimpse of the different rationales applied in choosing a particular ML approach. New ML methods are constantly being developed and often custom ML models are needed depending on the data structure and the problem at hand.

ML is making major and rapidly increasing changes to our field. While ML is typically viewed as a ‘magic wand’ or ‘black box’ to obtain desired results, without understanding the principles, the potential to encounter difficulties cannot be avoided. Potentially, the largest issue with ML is data unavailability. It is common for large data sets to have missing values, or the data needs to be converted to different forms (i.e. words to numbers). Additionally, data tends to be specific to a certain population and, overall, does not reflect a larger population. Lack of data diversity leads to ML models being trained for only specific tasks that cannot generalise to a broader population.

While there are many obstacles for ML in cardiac EP to overcome, the potential of ML is unprecedented. With proper understanding, our field is poised to be revolutionised by ML. Clinical decision-making involving ML is expected to become a more powerful force in combating rhythm disorders and heart disease, as ML algorithms will be better able to predict risk and diagnose patients accurately.