A Review of Personalised Cardiac Computational Modelling Using Electroanatomical Mapping Data

The general principles of cardiac electrophysiology (EP) have been studied for over a century, providing strong theoretical foundations upon which contemporary clinical management of arrhythmias is founded.^1,2 Contemporary clinical EP typically requires physicians to generate an electroanatomical model and commonly uses measurements of activation across the anatomy to diagnose, prescribe and provide therapy in the form of targeted ablation therapy. However, the treatment of AF, and even atrial flutter, is uncharacteristically generalised to anatomy.^3,4 The standard anatomically-based treatment for AF, which isolates the pulmonary veins, provides only moderate performance in achieving long-term freedom from AF, particularly in patients with persistent AF.^5,6

AF is characterised by chaotic and non-synchronised waves of depolarisation propagating throughout the atrial syncytium. This degree of asynchrony prevents traditional fixed-reference-based timing measurements that are nearly ubiquitous in basic and clinical EP, limiting the ability to observe and characterise the pathophysiology of AF and ultimately stifling the efficacy of patient-specific therapy in the past.⁷ However, large quantities of electroanatomical mapping (EAM) data are now available, together with new analysis techniques, with the potential to improve mechanistic understanding and treatment approaches through computational modelling.⁸

Computational modelling has long been used to improve our understanding of the underlying mechanisms that initiate, sustain and modulate complex arrhythmogenic substrates.⁹ For example, evidence from a right ventricular computational model was used by Hoogendijk et al. to investigate the current-load mismatch phenomenon in the sub-epicardium of patients with Brugada syndrome (BrS) that leads to alterations in excitation wavelength and, ultimately, elevates arrhythmia risk.^10,11 In addition, simulations generated through cardiac computational models have been used to predict phenotypes of a wide range of pathologies, such as acute ischaemia, BrS, long QT syndrome, MI and AF, to name just a few.^12,13

Personalised versions of these computational models may be used to predict individual patient response to ablation therapy, to predict patient trajectories, to guide individualised pharmacological treatment or for in silico trials. The patient-specific models can be personalised to different degrees using data from imaging or EAM. Specifically, creating personalised models of a patient’s cardiac EP requires several key components: an accurate geometric representation of the patient’s anatomy, an ability to characterise a patient’s electrophysiological substrate, a computational model of propagation, a method to calibrate the computational model to patient conduction properties and an assessment of the uncertainty associated with measurement and parameterisation of the model. This review will summarise the recent advancements in the personalisation of atrial EP modelling using EAM data with a particular focus on progress made in the last decade in the field of model personalisation and calibration.

Personalised Geometry

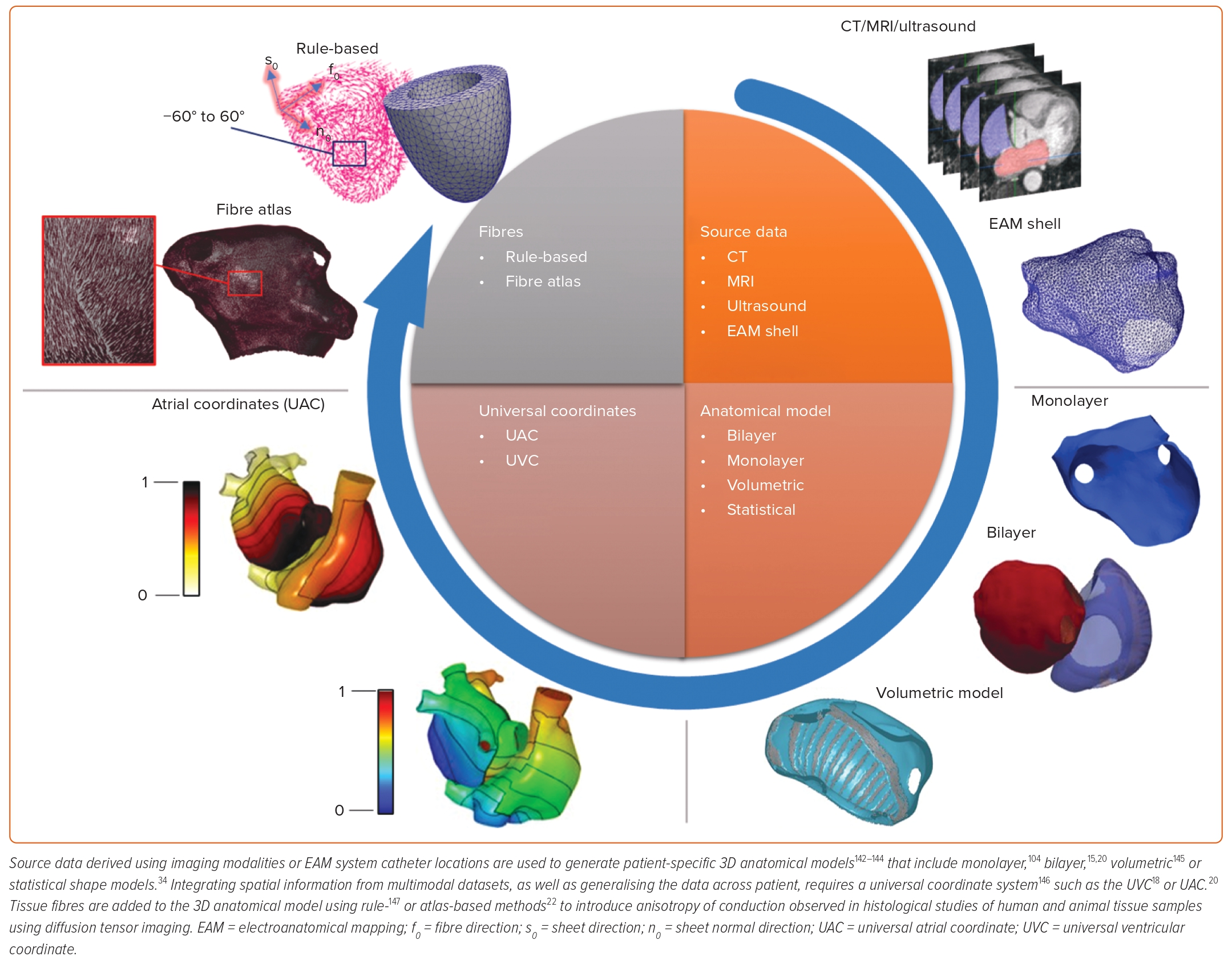
Anatomically realistic geometries for personalised simulations of cardiac pathologies typically require either 3D imaging data, including CT, MRI and ultrasound, or anatomies constructed from catheter navigation within an EAM system during an EP procedure. The EAM data are segmented and meshed to create an anatomical model represented as either a single surface (a monolayer model), coupled endocardial and epicardial surfaces (a bilayer model) or a 3D volumetric model. An alternative technique to create an anatomical model that does not require patient-specific imaging data is to use a statistical shape modelling approach that generates anatomies within the ranges expected across a population.¹⁴

To improve the model correspondence with clinical recordings, anatomical models may be augmented with specialised anatomical structures (such as the sino-atrial node, Bachmann’s bundle, crista terminalis and pectinate muscles) and inter-atrial structures in biatrial geometries, as well as outflow tracts and the Purkinje system in the ventricles.^15–17 These structures may be registered from an atlas using a standard coordinate system to map spatial information between anatomical meshes; for example, the universal atrial coordinate and universal ventricular coordinate systems.^18,19

Universal coordinates are a visualisation technique and also a coordinate system for the registration and construction of patient-specific anatomical models. In addition to realistic anatomy, the fibre orientation of myocardial tissue may be encoded in the personalised geometry, typically using rule- or atlas-based methods using universal coordinate systems.²⁰ Besides rule- or atlas-based methods that rely on diffusion tensor imaging, techniques have been developed to estimate cardiac fibres and anisotropy of conduction based on EAM data recordings.^21,22 These methods for geometry personalisation have successfully produced single-chamber as well as bi-atrial, bi-ventricle and four-chamber heart anatomies for personalised simulations.^14,23 An example workflow for generating personalised cardiac geometries, along with major types of anatomical models, is depicted in Figure 1.

Mapping Individualised Electrophysiology

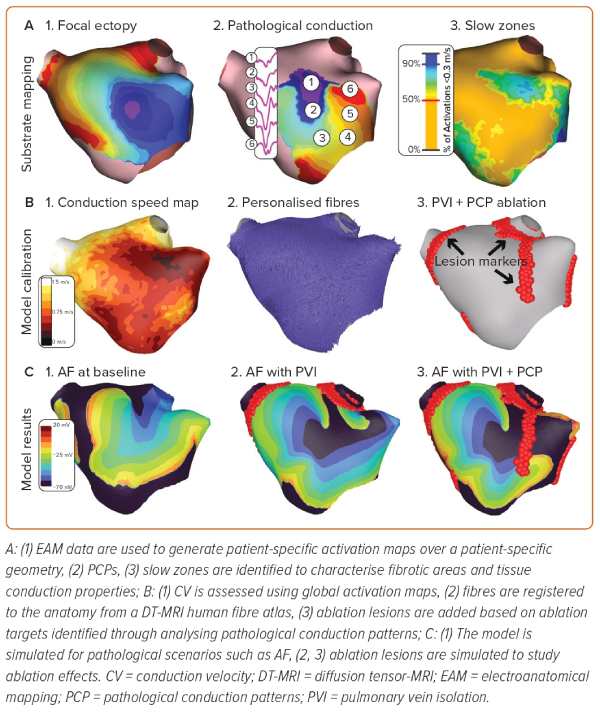
Personalised anatomical information may be augmented with detailed functional and structural information derived from EAM data or other imaging systems. These data enable characterisation of a patient’s pathophysiology through strictly structural means (e.g. fibrosis imaging), surrogate electrical measures (e.g. low bipolar voltage), or interrogation of the activation sequence (e.g. conduction velocity [CV]; Figure 2).

Fibrosis Imaging and Bipolar Voltage Mapping

Fibrosis is a fundamental process observed in cardiac re-modelling and is considered to be a key contributor to cardiac pathologies. Low voltage mapping during electroanatomical catheter ablation procedures is used as a surrogate marker to identify and map fibrotic cardiac substrates.^24,25 Modelling of fibrosis in regions identified through imaging and voltage-based (surrogate) techniques has been attempted in the past decade for better understanding and personalised treatment of cardiac arrhythmias.^26,27 Such biophysical fibrosis models incorporate changes introduced at the membrane, cellular and tissue level.²⁸ For example, the down-regulation and lateralisation of connexins (gap junctional protein) at the membrane level is incorporated in the personalised models either through reduction in coupling strength between cells or an increase in anisotropy ratios along with reduction in CV.^19,29,30 At the cellular level, fibrosis personalisation includes assigning myofibroblast properties to a percentage of elements, with a random distribution, within the identified fibrotic regions. Deposits of excess collagen at the tissue level have been introduced into computational models using layers of electrical isolation in a coarse 2D mesh, achieved via element decoupling, or a percolation method that removes elements as a probabilistic function of late gadolinium enhancement (LGE)-MRI intensity.^19,27

Characterising Personalised Propagation

Local Activation Time Annotation

Annotation of local activation times (LATs) on cardiac electrograms (EGMs) estimates the time that underlying or nearby tissue depolarises (or activates) at a recording site.^31,32 This estimate of LAT is repeated over space, either sequentially, simultaneously or a combination of both, to build a LAT map over a given anatomical structure. Clinically, intracardiac EGMs are acquired and processed using EAM software to build LAT maps that are used by clinicians to diagnose and treat arrhythmogenic sites and pathways.³² Accurate annotation of LATs in the clinic enables patient-specific diagnosis and treatment, as opposed to anatomical-only ablation approaches (such as pulmonary vein isolation).³³ As such, the ability to successfully treat arrhythmias and to generate personalised models is intrinsically dependent on the annotation accuracy of activations on each EGM recording; hence, this process occupies a fundamental step in EP personalisation pipelines.^34,35 However, the technique with which LAT is annotated varies substantially throughout the literature.

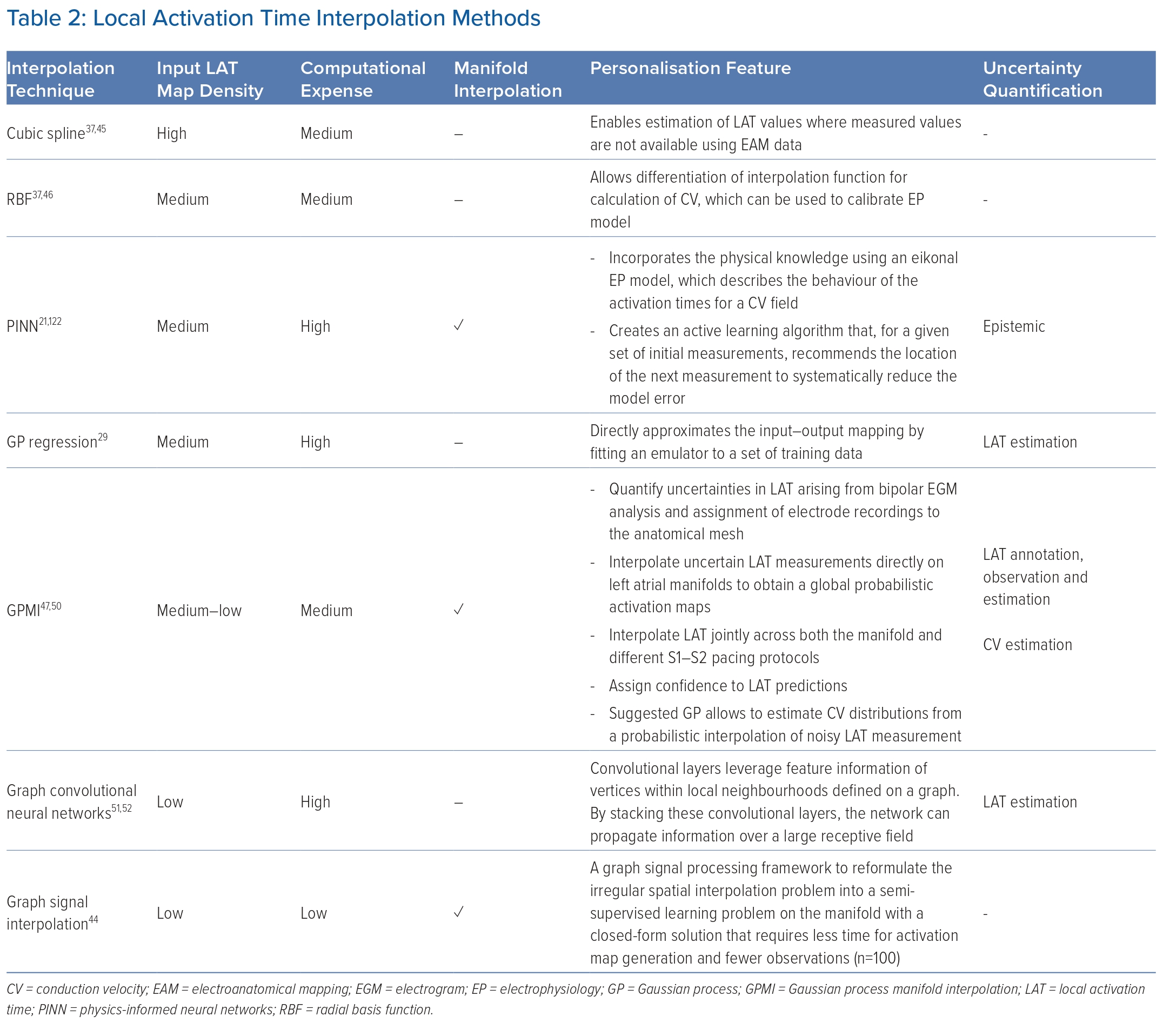
The most common and well-validated technique for annotating the LAT on unipolar EGMs uses the maximum negative gradient.³⁶ LAT annotation for unipolar and bipolar EGMs using maximum gradient, signal morphology, wavelet decomposition and other signal processing techniques developed during the past decades has been previously reviewed by Cantwell et al.³⁷ The clinical environment can make robust and reliable annotation of activation using these earlier techniques alone challenging, motivating the recent development of several innovative approaches. These include probabilistic, hybrid and inverse methods that aim to mitigate the primary sources of error encountered when annotating LATs: far-field signal artefacts in unipolar EGMs, orientation ambiguity in the case of bipolar EGMs and uncertainty associated with acquiring intracardiac measurements.^38–42 Table 1 lists techniques organised by category, along with the expected advantages that these approaches can provide towards model personalisation.

Interpolation of Activation Time Maps

Activation map construction is the result of a combination of steps, in which each step has an important impact on the final map. Along with signal annotation, activation time interpolation is an important (and often overlooked) step.⁴³ LAT interpolation remains an open and challenging research problem for several reasons. First, LAT recordings may be sparse and limited in resolution, so it is not currently possible to clinically record EGMs in all regions of the anatomy being personalised. In addition, the data are irregularly sampled with respect to the anatomical mesh.

Additional challenges for model personalisation include that each patient has both a unique cardiac anatomical structure and a distinct electrical activation pattern that must be taken into account to obtain an accurate LAT map. Furthermore, the surface of the heart is an irregular domain that is hard to represent mathematically and leverage for interpolation.⁴⁴

However, in contrast to signal annotation, users cannot currently modify interpolation schemes in clinical practice, making their impact more difficult to study. Various interpolation schemes have already been reviewed, along with their effects on EAM.^37,45–48 A comparison of current techniques aimed at the reconstruction of activation maps using sparse EAM recordings is shown in Table 2.^44,49–52

Conduction Velocity Estimation

CV is one of the most important metrics for assessing and personalising cardiac activation patterns. Activation maps generated through annotation and interpolation are used as the input for the assessment of CV. Available CV estimation methods have been previously reviewed by Cantwell et al.³⁷ Challenges associated with CV computation were covered by Han et al., and recent CV estimation techniques were compared by Nagel et al. and Good et al.^47,53–55 Reviews on patient-specific models also consider CV an important determinant of model personalisation.^56–58 A recent comprehensive review of clinical tools, algorithms and approaches by Coveney et al. classified available techniques into local, global and inverse methods, with detail on the advantages and disadvantages of each.⁴⁷ As such, a huge body of literature on CV spans across a number of recording and measurement modalities, including EAM, optical mapping, ECG imaging, torso tank experiments, multi-electrode socks and arrays, plunge needles, etc. A detailed comparison of the techniques and approaches for the assessment of CV is beyond the scope of this review; however, recent methods used in current personalised models include inverse eikonal methods, omnipolar EGM-based techniques, probabilistic methods and streamline-based techniques.^50,59–62 Previously reviewed methods commonly used in personalised models include radial basis functions, gradient methodologies, the use of isochrones and wavefront fitting methods.^35,47

Contemporary Proprietary Techniques

Along with the aforementioned techniques, automatically annotated LAT maps generated from EAM systems have also been imported directly into model personalisation pipelines.^34,35,63 Example LAT annotation systems include the advanced reference annotation algorithm in CARTO 3 V7 (Biosense Webster), AcQMap (Acutus Medical) charge density (CD) mapping, and RHYTHMIA HDx LUMIPOINT (Boston Scientific).

Although a clinical trial to compare these competing technologies is yet to be attempted, the performance of these algorithms regarding the accuracy of LAT annotation has been evaluated in a number of separate randomised clinical trials. For instance, clinical trials of the advanced reference algorithm (CARTO 3 V7), which uses a weighted reference algorithm across multiple electrodes to optimise reference annotation, demonstrated that this algorithm outperformed legacy algorithms and expert clinician diagnosis for 17 categories of both atrial and ventricular arrhythmias including AF, atrial flutter and VT.⁶⁴

Another recent international multicentre study MANual versus autoMATIC found that the CARTO 3 wavefront tracking algorithm demonstrated higher procedural efficiency compared with conventional, manual annotation carried out by expert operators, when applied to premature ventricular complex ablation.⁶⁵ The RHYTHMIA HDx LUMIPOINT software, which uses a ‘group reannotation’ feature, displayed improved accuracy of LAT automatic annotation in a clinical study carried out to identify earliest activation in idiopathic right ventricle outflow tract ventricular arrhythmias.⁶⁶ The Acutus Medical CD-based multi-position non-contact mapping produced highly accurate maps equivalent to gold standard contact mapping in 3 minutes of procedural time during clinical trials carried out to identify atrial tachycardia mechanisms and ablation sites.⁶⁷ Interesting developments make automatic LAT annotation a subject of expanding research interest that may lead to better and improved personalisation of computational models.

Models for Simulating Cardiac Electrophysiology

A variety of propagation models of EP are employed to simulate different arrhythmias, for mechanistic investigation, or to predict treatment response. The aforementioned models, including their advantages and limitations, have been discussed in several reviews. These models can be broadly classified into the following main categories based on their type and level of complexity:

Cellular and sub-cellular level models: this category is fairly broad and covers a variety of ordinary differential equations-based models that provide a mathematical description of the physiology of the cardiac cells and transmembrane potential.⁶⁸ These enable simulations of ionic currents, channels, gating variables, pumps, exchangers, calcium cycling and other cellular/subcellular functions using Hodgkin–Huxley- and Noble-type formulations.⁶⁹

Reaction diffusion type models: founded on Maxwell’s equations and the volume conductor theory, the reaction-diffusion type bidomain and monodomain model simulate propagation of the transmembrane potential.⁷⁰ These comprise a pair of coupled partial differential equations coupled with a suitable set of ionic current cellular ordinary differential equations, enabling us to model the action potential and the diffusion of current through the myocardial tissue.^71–74

Reduced-order models: another type of model is reduced order versions of the full order bidomain equations.^75,76 For example, eikonal models are based on macroscopic kinetics of the EP wavefront propagation and provide an efficient way of computing arrival times of depolarisation wavefronts in the myocardium. Variants of the eikonal type models that have been used in personalised models include reaction-eikonal and diffusion-reaction-eikonal.⁷⁷

Cellular automata: cellular automata models follow a set of rules to simulate electrical propagation. Previous applications include assessing the risk of arrhythmia in patients who have had an MI.⁷²

Limitations and Challenges

While the predictive nature of personalised electrophysiology models can immensely contribute towards developing tools to advance the precision and efficacy of AF treatment, the following limitations pose substantial challenges.

Simplified representations: despite significant progress in EAM-based modelling of personalised organ-level EP propagation, such as ionic cellular currents and action potentials, cellular calcium dynamics, model-based reconstruction of EGMs and sensitivity analysis linking cell to whole organ mechanisms, the existing models still introduce certain simplifications in cardiac tissue physics and may not capture the full complexity of arrhythmogenic substrates.^9,68,78,79 For example, the question of how to accurately model different types of fibrosis has not been satisfactorily answered;⁷⁸ another example is related to modelling of necrotic infarct regions where the assumption of a pure insulator neglects important passive properties of myocardial scar core despite clinical and in vitro evidence.⁸⁰ Similarly, simplified assumptions related to simultaneous ablation of lesions, growth and remodelling of fibrotic tissue and modelling of microstructure at spatial scales close to the cellular scale are substantial modelling challenges.^81,82

Parameter sensitivity: existing models depend on numerous parameters and small variations in these parameters can lead to significant differences in model predictions.^79,83 Accurate parameterisation can be challenging. Further details on available parametrisation strategies have been discussed at length in the next section (Approaches to Model Calibration), which addresses model calibration techniques.

Lack of spatial detail: many models are 1D or 2D, which may limit their ability to account for spatial variations in cardiac EP. Extensive arrhythmogenic substrates are complex and 3D, and this simplification can miss important phenomena. Pericardial substrates need to be localised exactly to be mapped and ablated, and distinguishing between the right and left ventricle may be challenging.

Temporal variability: cardiac properties may change on a beat-to-beat basis in response to changes in the autonomic system, making the choice of input data for calibration challenging.

Limited validation: validation of these models can be challenging due to the difficulty of obtaining comprehensive experimental data. This can make it hard to determine the accuracy and reliability of the models. Efforts to define methods to assess patient-specific model credibility are now being developed, such as the recently issued Food and Drug Administration guidelines and recommendations made by the research community.^84,85

Computational intensity: simulating cardiac EP at high spatiotemporal resolution requires significant computational resources, making real-time or large-scale simulations challenging. Reduced order and simplified eikonal models have been proposed to allow model generation time suitable for clinical timelines.^86,87 The accuracy of such eikonal models and techniques, however, requires validation against full-scale models and clinical data.

Model and data uncertainty: EAM data collection and suitability for model generation are other practical limitations associated with model personalisation. In this regard, the spatial resolution of recorded EAM data often limits model fidelity. EAM recordings collected before ablation therapy are mostly focused on specific regions of atria and uncertainty about surface recordings at unmapped regions exist. This also raises data-related uncertainty and can limit accurate parametrisation of cardiac tissue where recordings are not available. There is often uncertainty in the choice of model equations and parameters, which can lead to a lack of confidence in model predictions, especially when extrapolating to different conditions or patient-specific cases.^88–90 A range of credibility assessment mechanisms/techniques/criteria for models personalised to patient data is required to quantify uncertainty and provide an index for the measure of confidence for use of a given model to serve clinical needs.^85,91

Complexity of tissue interactions: models often do not account for the interaction of cardiac tissue with other parts of the body, such as the nervous system, which can be important in certain pathological conditions. Personalised models based on EAM may eventually require a modelling interface with other organs. An Ecosystem for Digital Twins in Healthcare (EDITH) has been laid out in this regard by the European Commission, with the aim of bridging the gap between separated single organ systems and a data-driven and knowledge-driven fully integrated multiscale and multiorgan whole-body twin.⁹²

Incomplete knowledge: our understanding of cardiac EP is not yet complete, and there are still many unknown factors and mechanisms that models cannot account for. For example, drivers of pathologies such as AF, fibroblast coupling and exact mechanisms of mechano-transduction channels are just a few such mechanisms that are still to be uncovered. Limitations associated with imaging of thin tissue structures and mapping of electrophysiological substrate also contribute towards our incomplete understanding of the EP of the heart.

Patient-specific variability: final challenges include that there is a huge range of inter-patient variability and that pathologies affect these measurements.^93–96 While models can be used for personalised medicine, individual patients may have unique characteristics that are not well-represented by general models. There is a drive towards population-based models to develop virtual cohorts of cardiac digital twins that can capture the heterogeneity associated with this challenge.^97–99

Ethical and practical limitations: clinical application of computational models may face ethical and practical challenges, such as the need for accurate data and regulatory approval.

Approaches to Model Calibration

The problem of calibrating tissue conductivity parameters and conduction anisotropy of personalised models using electroanatomical data is challenging due to high dimensionality, nonlinearity and stochasticity.⁷⁷ Only three fully experimentally determined datasets of the four bidomain conductivities in ventricular tissue exist, while experimentally measured atrial tissue conductivity parameters have not been reported.^100,101 For modelling purposes, it is customary to use these conductivity values as a reference value, or in lieu of accurate conductivity values, researchers often tune the conductivity values to ensure that the conduction velocities are in the range of 30–80 cm/s.^73,102,103 The problem is further compounded due to model and measurement uncertainty.⁸⁸

To overcome the above limitations, there is a drive towards discovering computationally efficient, faster and precise means to calibrate tissue EP properties to identify the mechanisms underpinning AF and to predict optimal therapy on a patient-specific basis.¹⁰⁴ In this regard, the traditional approach towards model personalisation is aimed at calibrating the conductivity diffusion tensor parameters, fibre directions and anisotropy of conduction using EAM data.^21,22,34,105 In addition to cardiac tissue conductivity calibration, the approach to calibrate tissue restitution properties leads to personalisation of the effective refractory period (ERP). Recently suggested methods also include probabilistic means to calibrate models to a range of parameters, which incorporates the effects of uncertainty. Various methods reported for calibrating cardiac EP models to EAM data recordings are covered in the following paragraphs.^38,88,106

Iterative Tuning

LATs, CV and LGE-MRI image intensity ratio (IIR) have been used to characterise atrial tissue conductivities to calibrate models to clinical observations (Figure 3).^107,108 The idea is to improve the agreement between clinical observations and simulations by using either LATs, CV or tissue IIR as inputs to fitting algorithms. These methods allow a global characterisation of tissue conductivity values based on clinical observations directly obtained from EAM or MRI mapping; however, a single map is insufficient to calibrate the anisotropy of propagation. Hence, typically, conduction anisotropy is prescribed based on average values.

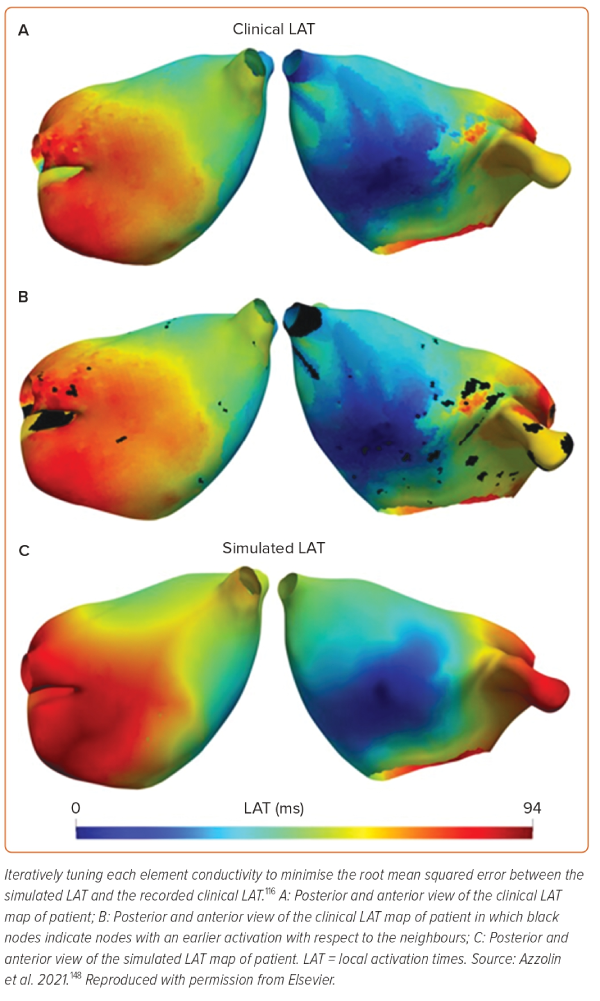
LAT-based calibration A recently proposed atrial personalisation pipeline called AugmentA suggests iteratively tuning the conductivity of each element in a mesh to minimise the root mean squared error between simulated LAT and the recorded clinical LAT.³⁴ In a related study, the AugmentA personalisation pipeline was used to perform personalised in silico ablation (PersonaAL) on a cohort of 29 patients to test 13 different ablation approaches.¹⁰⁵

CV-based calibration Assuming a continuously propagating planar wavefront along a given direction, Costa et al. proposed a method that is designed to iteratively retrieve all three bulk conductivities from 1D cable simulations by tuning them to match atrial or ventricular CV.¹⁰³ This fitting technique was used in later work for personalising a left atrial model by tuning conductivity values based on CV.¹⁰⁹ To model atrial propagation, a 3-mm radius sphere was stimulated at a fixed location. A range of conductivity values were tested, with the LATs at pre-defined points recorded on the spherical surface. For each value of the conductivity, the CV triangulation algorithm was used to estimate values of conduction speed within each of the three triangles. The three conduction speeds were averaged and plotted against the conductivity to obtain a relation between conduction speed and conductivity values. A similar approach was used for atrial geometries by Pagani et al.³⁵

IIR-based calibration: several other studies, such as Optima, rely on atrial IIR values for characterising atrial tissue fibrosis^108–110. In addition, an extension to the AugmentA study has suggested a number of approaches for personalising models through use of atrial IIR.¹⁰⁵ In one such method, the model is calibrated by discretely applying CV values depending on the IIR value following Beach et al.¹¹⁰ In this case, IIR<1.2 was used to prescribe normal/healthy tissue (longitudinal CV of 1 m/s), whereas, 1.2≤IIR<1.32 was modelled as interstitial fibrosis (0.7 m/s CV). Tissue with IIR>1.32 was classified as dense fibrosis (0.6 m/s CV). Another method uses a regression model for relating CV to IIR values.¹⁰⁵

Inverse Eikonal Simulations

In the early 1990s, work by Franzone et al. and Keener elucidated the relationship between the eikonal equation and the bidomain model.^71,111 Since then, diffusion and curvature-based eikonal models of EP have been used as an efficient way of computing arrival times of the depolarisation wavefront in the myocardium; the potential limitations have also been studied extensively.^95,96,112

Inverse eikonal simulations provide a computationally inexpensive way to estimate macroscopic metrics of interest, such as cardiac conductivity, activation times and fibre directions. To solve inverse eikonal models using EAM data, Chinchapatnam et al. suggested a multilevel approach to the conduction estimation problem, Cedilink et al. proposed parametrising eikonal simulations through the use of a genetic algorithm and Grandits et al. developed a fast iterative method minimisation algorithm for identifying governing parameters of the cardiac CV field and earliest activation sites.^112–114

A recently proposed technique called Personalized Inverse Eikonal Model from Cardiac Electro-Anatomical Maps (PIEMAP) implements an inverse problem in which the optimal conductivity tensor field is selected such that the mismatch between recorded activation times and the simulated activation times is minimised on the domain in the least-squares sense using a fast iterative method.¹¹⁵ Fibre directions and CV are estimated through eigen decomposition of the conductivity tensor, with the largest eigenvalue showing CV in the fibre direction. In a proof-of-concept extension to this work, PIEMAP was used to reconstruct activation patterns of atria for nine symptomatic paroxysmal or persistent AF patients.¹¹⁶ While a good correlation was observed (r >0.93 in seven patients and modest r=0.62 and r=0.74 in two patients), the technique is amenable to inaccuracies in the case of ectopic activity, multiple breakthroughs or noise in the earliest activation. Moreover, the optimisation problem is convex and nonlinear with a strong dependence on the choice of initial condition of the conductivity tensor.

Data Assimilation and Inverse Techniques

Data assimilation techniques can be used to estimate tissue conductivity parameters that cannot be measured or observed directly, especially in patient-specific settings. A variational procedure achieves this assimilation by finding orthotropic conductivity values that minimise the mismatch between cardiac EAM data and the results of an eikonal, a monodomain or bidomain solution.^117,118 Formally, this leads to an inverse problem of EP discussed by MacLeod et al. and Dössel et al. and later adapted for determining cardiac conductivities in the monodomain model.^119,120

Conduction Anisotropy Assessment

Statistical and Geometric Methods

Statistical techniques such as least squares have been used in combination with geometric modelling for estimating fibre direction and conductivity ratios from LATs recorded during the EAM process. Assuming the propagation wavefront as planar, circular or elliptic, the idea is to use recorded activation time and distances to estimate the conduction anisotropy ratio and dominant propagation direction (fibre angle) over an EAM mesh.

Making use of single or multiple activation maps, Roney et al. proposed an algorithm for estimating local conduction anisotropy and fibre directions.²² The algorithm works for any arrangement of points on the atrial surface and for any pacing location. Ellipse fitting was performed on CV vectors from two clinical activation maps to predict the longitudinal and transverse CV, assuming an atlas distribution of fibres, or to three activation maps fitting the fibre distribution. The proposed algorithm is not limited to atrial data but is also applicable to ventricular data in the instance that transmural activation is not considered.

Based on a similar idea, a method proposed by de Vries et al. calculated local conduction slowness, represented as points in the conduction slowness space.¹²¹ For a homogeneous area of tissue, these points roughly align with an ellipse. The fibre direction and conductivity anisotropy ratio can, therefore, be estimated from an activation map by fitting an ellipse to the conduction slowness points using a least squares approach.

Deep Learning and Physics-informed Neural Networks

Development of deep learning-based physics-informed neural networks (PINNs) for the solution of forward and inverse partial differential equations have opened new avenues to encode eikonal physics in the network loss function for computationally efficient and accurate means of CV and tissue conduction assessment using EAM mapping data.¹²² For estimating fibre anisotropy, the objective is to identify the ratio of tissue longitudinal and transverse conductivities such that the corresponding activation map, resulting from the solution of the anisotropic eikonal model, will closely reproduce the observed data. The method approximates both the activation map and the conductivity values using a feedforward neural network using a loss function, which comprises of the sum of activation time accuracy (the difference of values between model predictions and clinical ground truth), the partial differential equation model accuracy and two regularisation terms that ensure that approximated data remains in agreement with the physics of EP.

Built on this idea, a recently proposed multiple map neural network technique, FiberNet suggests the use of multiple neural networks for increased accuracy and penalising the loss function only partially for achieving a good balance between complexity and efficiency.²¹ This method estimates the complete CV tensor from a set of EAM maps. This is achieved by simultaneously fitting multiple neural networks to multiple electroanatomical maps while using a common network that predicts the CV tensor at different locations. The decomposition of the tensor simultaneously provides a patient-specific estimate of the fibre directions, conduction anisotropy and conduction velocities.

PINNs are constrained to respect any symmetries, invariances, or conservation principles originating from physical laws that govern the observed data, as they are modelled by eikonal models of EP. The results of fibres produced by this method were tested against synthetic and diffusion tensor MRI datasets. The method produced a root mean squared error of 2.09 ms in the predicted activation.

In another recent work by Ntagiantas et al., the spatial distribution of tissue conductivity is directly inferred from an array of concurrently acquired contact EGMs using a deep neural network, based on a modified U-net architecture.¹²³ The network is trained to estimate location of the scar and conductivity of the tissue. Based on synthetic data, the method provides a proof of concept that EGM recordings can be used in conjunction with deep neural networks to estimate conduction properties of the underlying myocardium.

Probabilistic Calibration

Probabilistic approaches show promise as a way to obtain personalised models while taking account of noise, sparseness and uncertainty intrinsic to EAM recordings. Workflows have been proposed to recover parameters from sparse EAM data of atria in which Gaussian processes (GPs) are used to represent parameter fields, and the posterior distribution of CV is inferred using Markov chain Monte Carlo.^50,106,124 The starting point of the workflow is a mesh representing the left atrium, and bipolar EGMs are recorded at different locations within the left atrium and at different pacing cycle lengths. From these observations, LATs are estimated at the electrode locations using a modified centre of mass method. The second step is to interpolate LAT across the left atrial mesh taking a set of uncertain measurements modelled as a GP. Having obtained a probabilistic interpolation of LAT, the third step is to calculate the inverse of the gradient in LAT to obtain an uncertain estimate of CV at each mesh vertex. The last step is to use these estimates to calibrate the EP model based on the workflow suggested by Coveney et al.¹²⁴ For recovering parameters fields related to tissue conductivity and restitution properties and to calibrated EP models, an extension has been suggested using latent GPs by Coveney et al.¹⁰⁶

Calibration of Tissue Restitution

Cardiac cells exhibit rate adaptation to allow the body to adapt to increased heart rates. This means that action potential duration and CV depend on the coupling interval between beats or the diastolic interval. There is a time after an action potential is initiated when a new action potential cannot be initiated, termed the ERP. Whether re-entry can be induced and AF properties both depend on the CV and ERP, and so calibration of ERP and tissue restitution is important for capturing patient-specific arrhythmia properties.

Estimation of ERP is accomplished through an S1–S2 pacing protocol using a measuring catheter in the clinic (or a simulated sensing electrode in silico), where ERP is the longest S2 coupling interval to produce an atrial capture. In general, action potential duration (APD) increases with increasing coupling interval and the relation between action potential duration and the preceding diastolic interval describes the APD restitution curve.¹²⁵ The latter has recently been the focus of considerable interest since the steepness of the initial part of the restitution curve plays an important role in electrical stability and arrhythmogenesis.¹²⁶ Calibration of tissue restitution is markedly different from calibrating tissue conductivity as, in this case, there is a need to calibrate ionic properties of the cellular model, which are largely not directly observable.¹²⁷ Some methods falling in this category have, therefore, made use of the modified Mitchell–Schaeffer model described by four parameters representing the characteristic time constant of four distinct phases of an action potential.¹²⁸

Conduction Velocity Restitution Curve Fitting

This approach makes use of an EP computational model to generate pre-computed CV and ERP restitution curves, which are fit to clinically recorded data to identify model parameters.¹²⁹ Using activation times measured with a PentaRay catheter and caused by a stimulus applied in the coronary sinus with a remote catheter, Corrado et al. fitted parameters of the modified Mitchell–Schaeffer model and the tissue conductivity to the recorded local CV restitution curve and estimated local ERP. The method was applied to five clinical cases; the spiral wave stability was analysed on a 5 cm² square homogeneous tissue slab and both stable and unstable self-terminating rotors were identified.¹³⁰ Recently, a workflow based on the same calibration approach has been used to generate a cohort of left atrial models that capture clinically measured patient-specific EP heterogeneity for data sets recorded from seven paroxysmal AF patients undergoing pulmonary vein isolation.¹⁰⁴

Restitution Curve Emulators

This approach is motivated by the need to perform probabilistic calibration with clinical data, such as restitution measurements. Restitution curve emulators (RCEs) are probabilistic models that can capture the shape and variability of restitution curves using principal component analysis and GPs.¹³¹ These probabilistic models can perform model exploration, sensitivity analysis and Bayesian calibration to noisy data. RCEs are built by decomposing restitution curves using principal component analysis. RCEs allow rapid and accurate prediction of CV, APD, and ERP restitution curves from model parameters.

Discussion

Innovative mechanistic EP studies have the potential to provide detailed characterisation of a patient’s electrophysiological substrate. For example, Honarbakhsh et al. recently investigated the relationship between rotational drivers, focal drivers, and structural remodelling.¹³² Such detailed datasets may be further used to calibrate personalised atrial models to investigate the individual and combined contribution of factors to patient-specific AF mechanisms and expected treatment outcomes.^80,105 Multiple studies have demonstrated that CV, action potential duration and their restitution properties vary both between patients and spatially across the atria.¹³³ Initial computational studies that varied action potential duration and CV from a baseline parameter set have shown that model predictions depend on these parameters.^19,134 For example, Deng et al. found that simulated driver locations changed when action potential duration and CV were changed within a small range of ± 10%.⁸³ As an extension to this, Macheret et al. showed that persistent AF simulations better matched clinical data when different conductivity values were simulated.¹³⁵ This broadly demonstrates both the variability of these metrics between and within patients, and the importance of these metrics on personalised model predictions, and yet most studies do not include calibration to EP measurements. In our review, we present the state of the art in model personalisation using EAM data, with the hope that groups can use and further develop the techniques presented here in their research.

The state-of-the-art computational modelling of EP has matured to a level where clinical trials of in silico ablation approaches and population models of in silico pharmacology testing are now being reported.^108,136 Research software ranging from imaging data analysis to EP data import and treatment planning has the potential to enable a fundamental translation from population-based approaches to patient-specific treatments of cardiac pathologies. Examples, such as OpenEP pipeline suggested by Williams et al., cemrgApp for cardiovascular imaging by Razeghi et al., biatrial modelling pipeline by Roney et al. and MusiCardio for treatment planning by Merle et al., are just a few among a widely diverse range of workflows beings developed.^137–140 The research landscape is continuously developing from cardiac digital twins to populations of cardiac models at scale, enabling large in silico trials. With a wide range of cellular-level EP models alongside a range of strategies for model generation and calibration, we hope that the computational and clinical community will devise standards and benchmarks, such as those suggested by Clayton et al. and Pathmanathan et al., for setting up a road map of implementation, from bench to bedside.^84,88 Computational models offer valuable insights into complex arrhythmias, such as BrS and AF, but have limitations, including oversimplification and challenges in real-time dynamics capture. Dynamic aspects of arrhythmic substrates in BrS and AF pose modelling challenges. Ongoing research is crucial to refine models and ensure clinical relevance. Ethical concerns, unanswered questions and the lack of direct clinical validation raise limitations. Despite these challenges, computational models – when validated and calibrated – contribute scientifically to advancing the understanding of EP. Collaboration between researchers and industry should aim at scientific knowledge enhancement rather than solely increasing industry activity. Ethical concerns regarding therapy require cautious interpretation and rigorous clinical validation.

Looking to the future, we hope to see translation to the clinical environment of several of the probabilistic calibration techniques presented here for restitution and conduction anisotropy. This will require careful consideration of the potential limitations of the use of EAM data for model calibration because of the invasive nature of the data and likely constraints on the model complexity and processing speed to use model predictions in the same procedure. Future research will investigate the effects of new mapping modalities, including omnipolar mapping, on personalised model construction and the transformation of anatomically personalised models to EP-personalised models, with the potential to guide treatment.¹⁴¹